線性迴歸：機器學習入門的關鍵概念

什麼是線性迴歸？

線性迴歸（Linear Regression）是機器學習領域中最基本且廣泛使用的監督式學習演算法之一。它的核心目標是通過尋找輸入的變量（特徵）和輸出的變量（目標）之間的線性關係，來預測未知數據的結果。也就是説，我們希望找到一條最佳的直線來描述輸入特徵和輸出結果之間的關聯性。這條直線不僅能解釋現有數據，還能有效地對未來數據進行預測。線性迴歸具有簡單且易於理解的特點，因此你可以在很多的綫上課程中發現很多教AI、ML的都是從線性迴歸開始的。

線性迴歸的數學表示

線性迴歸模型的數學形式方程：

y = b + w1*x1 + w2*x2 + ... + wn*xn

• y：代表我們想要預測的目標變數，也稱為輸出值（因變數/應變數）。
• b：是偏差項（bias），它用來調整模型的預測結果，確保模型能夠更好地與資料吻合。
• x1, x2, ..., xn：這些是輸入特徵，表示影響輸出結果的各種自變數。
• w1, w2, ..., wn：這些是對應於每個輸入特徵的權重參數，模型通過學習這些權重來確定每個特徵對預測結果的影響程度。

線性迴歸的目標與最小二乘法

線性迴歸的核心目標是找到一組最佳的參數（w*），使得預測值 y 與真實值之間的誤差最小化。為了達成這個目標，我們通常使用一種稱為最小二乘法的方法來優化模型參數。

最小二乘法的基本概念是最小化所有數據點與回歸直線之間的垂直距離的平方和，也稱為殘差平方和（Residual Sum of Squares, RSS）。具體來說，我們希望找出一組w 參數，使得所有預測值與實際值之間的誤差平方和達到最小：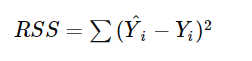

除了最小二乘法之外，還有其他常見的衡量預測誤差的方法，例如：平均絕對誤差（MAE）、均方誤差（MSE）、根均方誤差（RMSE）。這些指標各自有不同的適用場合，可以根據具體情況選擇使用：

• MAE: 每個誤差的實際絕對值加總。
  
• MSE: 強調大誤差的影響，對於大誤差較敏感。
  
• RMSE: MSE 的平方根，更容易與原資料單位對齊。
  

線性迴歸的實際應用

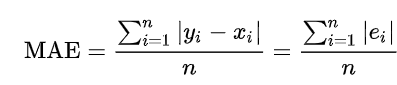
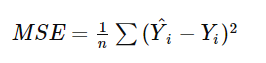
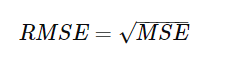
線性迴歸在各行各業中得到了廣泛應用，以下是一些具體的例子：

1. 房價預測：根據房屋的特徵（如面積、地點、樓層等）來預測房價
2. 銷售額預測：通過分析廣告投入、季節性波動等因素，預測某一時間段的銷售額
3. 股票價格預測：通過歷史資料和經濟指標，利用線性迴歸來對股票價格進行預測